車の振動を理解する第一歩:1自由度系

車のことを知りたい
『1自由度系』って、どういう意味ですか?難しそうです…

車の研究家
簡単に言うと、物の動きを一つの数値で表せるものだよ。例えば、天井から吊るされたおもりの動きは、天井からの距離だけでわかるよね?これが1自由度系なんだ。

車のことを知りたい
なるほど。おもりの位置が一つでわかるから、1自由度系なんですね。他に例はありますか?

車の研究家
ブランコはどうかな?ブランコの動きも、地面からの高さだけで大体わかるよね。もちろん、完璧ではないけれど、単純な動きを考えるときは1自由度系として扱えるんだ。複雑な動きをするものは自由度が増えて、たくさんの数値で表す必要があるんだよ。
1自由度系とは。
機械の動きを考える上で、『1自由度系』という用語があります。これは、機械の場所をたった一つの数字で表せることを意味します。例えば、天井からバネで吊るされたおもりを考えてみましょう。おもりは上下にしか動かず、その位置は天井からの距離だけで決まります。このように、一つの数字で位置を表せるものが1自由度系です。
機械の動きを調べる時、この1自由度系が基本となります。もし自由度が増えると、動きは複雑になり扱いが難しくなります。しかし、『モード解析』という方法を使うと、複数の自由度を持つ複雑な動きでも、いくつかの1自由度系の組み合わせとして考えることができます。つまり、機械の振動を理解するためには、まず1自由度系を理解することが重要なのです。
自由度とは

機械の動きを捉える上で、『自由度』という考え方はとても大切です。これは、機械の動き方を決めるために必要な、個別の位置の情報の数のことを指します。簡単に言うと、機械がどれくらい自由に動けるかを示す指標です。
例えば、糸で吊るされた重りを考えてみましょう。この重りは、糸に沿って上下にしか動くことができません。重りの位置を知るためには、地面からの高さだけを測れば十分です。つまり、この重りの動きは一つの情報で決まるので、一自由度と言えます。
一方で、空を飛ぶ飛行機を考えてみましょう。飛行機は上下左右前後へと自由に移動できます。さらに、機首の向きを変える回転運動(ヨー)、翼を傾ける回転運動(ロール)、そして機体を傾ける回転運動(ピッチ)も可能です。これらの動きを全て把握するためには、六つの情報が必要となるため、飛行機は六自由度と言えます。
自動車の動きは複雑ですが、揺れのような特定の動きだけに注目する場合は、一自由度として扱うことができます。たとえば、でこぼこ道を走るときに車が上下に揺れる場合、その揺れの大きさを知るだけで、だいたいの動きを把握できます。このように、注目する動きを絞ることで、複雑な動きを単純化して理解しやすくなるのです。
自由度は機械設計において重要な役割を果たします。設計者は、機械の用途に合わせて適切な自由度を設定することで、機械の動きを制御し、目的の動作を実現するのです。
| 物体 | 自由度 | 説明 |
|---|---|---|
| 糸で吊るされた重り | 1 | 地面からの高さで位置が決定 |
| 飛行機 | 6 | 前後、左右、上下の移動、ヨー、ロール、ピッチの回転 |
| 自動車(揺れのみ) | 1 | 上下の揺れの大きさで動きを把握 |
| 自動車(通常) | 複雑 | 様々な動きが可能であり、単純化して自由度を扱う場合もある |
ばねと錘の振動

物を吊るすための巻かれた金属線である、ばね、を考えてみましょう。このばねに重りを繋げると、重りの重さでばねは伸びます。重りを下に引っ張ってから手を離すと、ばねの力によって重りは上下に動き始めます。これがばねと重りの振動です。この振動は、重りの位置だけで動きが決まるため、一自由度系の振動と呼ばれます。
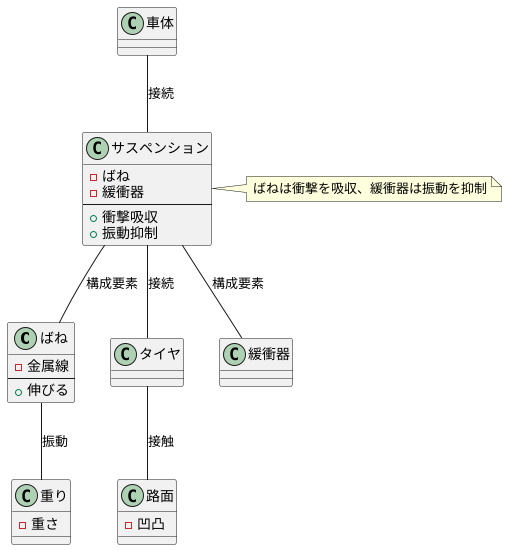
この単純なばねと重りの振動は、実は自動車の乗り心地を大きく左右する部品である、サスペンションの動きを理解する上で非常に重要な基礎となります。サスペンションは、車体とタイヤの間をつなぐ部品で、路面の凸凹からくる衝撃を吸収し、車体の揺れを抑える役割を果たしています。サスペンションは主に、ばねと、動きを抑制する部品である緩衝器の二つの部品から構成されています。ばねは路面からの衝撃を吸収し、緩衝器はばねの振動を抑え、滑らかに収束させる働きをしています。
車がデコボコ道を走ると、タイヤは路面の凹凸に合わせて上下に動きます。このタイヤの動きがサスペンションに伝わり、ばねが伸び縮みすることで衝撃を吸収します。もしサスペンションが無ければ、路面からの衝撃が直接車体に伝わり、乗員は激しい揺れを感じてしまいます。また、タイヤが路面から離れてしまうと、ハンドル操作やブレーキ操作が効かなくなり大変危険です。サスペンションはこれらの問題を防ぎ、快適で安全な運転を可能にしています。このサスペンションの動きを単純化して考えると、ばねと重りの振動モデルと同じように理解することができます。車体を重り、サスペンションのばねをばね、そして緩衝器の効果を加えることで、より現実に近い車の挙動を解析することが可能になります。
車体振動への応用

乗り物の快適さは、車体の揺れ具合と深く関わっています。道路の凸凹によって生じる振動が車体に伝わり、乗っている人は揺れを感じます。この揺れをいかに小さくするかが、快適な乗り心地を実現する鍵となります。
車体振動を理解する上で、1自由度系モデルは基本となります。これは、車体を一つの質量として捉え、ばねとショックアブソーバー(減衰器)で支えられた単純なモデルです。このモデルを用いることで、車体振動の基本的な特性を把握できます。
乗り心地を良くするためには、ばねとショックアブソーバーの特性を調整することが重要です。ばねの硬さを調整することで、路面からの衝撃の吸収具合が変わります。柔らかいばねは衝撃を吸収しやすくしますが、車体の揺れ幅が大きくなることもあります。反対に硬いばねは、揺れ幅を抑える一方、路面からの衝撃を伝えやすくなります。
ショックアブソーバーは、揺れの収まり具合を調整する役割を果たします。ショックアブソーバーの減衰力を大きくすると、揺れは早く収まりますが、路面からの衝撃を吸収しにくくなります。逆に減衰力を小さくすると、揺れは収まりにくくなりますが、路面からの衝撃を吸収しやすくなります。
最適な乗り心地を実現するためには、ばねの硬さとショックアブソーバーの減衰力のバランスが重要です。路面状況や車の用途に合わせて、これらの特性を調整することで、快適な乗り心地を実現できます。例えば、高級車では、路面からの振動を効果的に吸収するために、柔らかいばねと適切な減衰力のショックアブソーバーが用いられることが多いです。一方、スポーツカーでは、走行安定性を重視するため、硬いばねと強い減衰力のショックアブソーバーが用いられる傾向があります。
| 要素 | 機能 | 特性調整による影響 | 例 |
|---|---|---|---|
| ばね | 路面からの衝撃吸収 |
|
高級車:柔らかいばね |
| ショックアブソーバー (減衰器) |
揺れの収まり具合調整 |
|
スポーツカー:強い減衰力 |
複雑な振動の解析

車は、多くの部品が組み合わさってできています。それぞれの部品は、ばねのように伸び縮みしたり、重りのように重さを持っていたり、摩擦によって動きにくくなったりと、様々な性質を持っています。これらの部品が組み合わさることで、車全体もまた、複雑な振動の性質を持つようになります。単純な一つのばねと重りの組み合わせだけでは、実際の車の振動を表現することはできません。
道路の凹凸もまた、車の振動に大きな影響を与えます。道路の表面は完全に平らではなく、大小様々な凹凸が存在しています。車がこの凹凸を乗り越える際に、様々な大きさや速さの振動が発生します。これらの振動は、単純な一つの波として表すことはできず、多くの異なる波が組み合わさった複雑な波として現れます。
このような複雑な振動を理解し、解析するためには、複数のばねと重りを組み合わせたモデルを考える必要があります。それぞれの部品の振動の性質を考慮し、それらがどのように相互作用するかを分析することで、車全体の振動の様子をより正確に捉えることができます。さらに、コンピューターを使った高度な計算方法を用いることで、複雑な振動をより詳細に解析することも可能です。
しかし、複雑な振動を理解するための出発点となるのは、単純な一つのばねと重りの組み合わせの振動です。この単純なモデルを学ぶことで、振動の基本的な性質、例えば振動の大きさや速さ、振動しやすさなどを理解することができます。そして、この基礎的な理解の上に、より複雑な振動の解析を積み重ねていくことができます。単純なモデルは、複雑な現象を理解するための重要な土台となるのです。
| 車の振動 | 詳細 |
|---|---|
| 部品の性質 | ばね(伸び縮み)、重り、摩擦など、様々な性質の部品が組み合わさっている。 |
| 道路の影響 | 道路の凹凸が様々な振動を発生させる。 |
| 振動モデル | 複数のばねと重りを組み合わせたモデルで、複雑な振動を解析する必要がある。 |
| 振動解析の基礎 | 単純な一つのばねと重りの組み合わせの振動が、複雑な振動を理解する土台となる。 |
より高度な振動解析

物が揺れる現象、つまり振動は、車を作る上で避けて通れない問題です。単純な揺れであれば、高校物理で学ぶような一つの塊が一つのばねで支えられた「1自由度系」で近似的に表現し、解析できます。しかし、実際の車はもっと複雑な構造をしています。そこで、より高度な解析手法が必要になります。複数の1自由度系を組み合わせた「多自由度系」を使うことで、現実に近い振動の様子を捉えることができるようになります。例えば、車体をいくつかの部分に分け、それぞれをばねと塊で表現することで、車体全体の振動をより正確に再現できます。
さらに、「モード解析」という手法も重要です。複雑な振動は、実は単純な振動の組み合わせでできています。モード解析では、複雑な振動をいくつかの固有の振動、「モード」に分解します。それぞれのモードは、特定の周波数と形を持っており、この形を「モード形状」と呼びます。モード解析を行うことで、どの部分がどの周波数で大きく揺れるのかが分かります。例えば、車が特定の速度で走行したときに、ハンドルが大きく振動する場合、その振動の原因となっているモードを特定し、そのモードの周波数やモード形状を解析することで、対策を立てることができます。
これらの高度な解析手法は、車の設計開発において欠かせません。車体の振動特性を予測することで、乗り心地を向上させたり、騒音を低減させたりすることができます。また、特定の部品が共振を起こし、破損するのを防ぐためにも、これらの解析手法は活用されています。例えば、エンジンの振動が車体に伝わり、不快な振動や騒音が発生するのを防ぐために、エンジンマウントの設計に振動解析の結果が用いられます。このように、振動解析は、快適で安全な車を作る上で、重要な役割を担っています。
| 手法 | 説明 | 用途 |
|---|---|---|
| 1自由度系 | 単純な揺れを表現。一つの塊と一つのばねで近似。 | 基礎的な振動解析 |
| 多自由度系 | 複数の1自由度系を組み合わせ、現実に近い振動を表現。車体を複数の塊とばねで表現。 | より高度な振動解析 |
| モード解析 | 複雑な振動を単純な振動(モード)に分解。各モードは特定の周波数と形状(モード形状)を持つ。 | 振動の原因特定、対策立案 |
まとめ

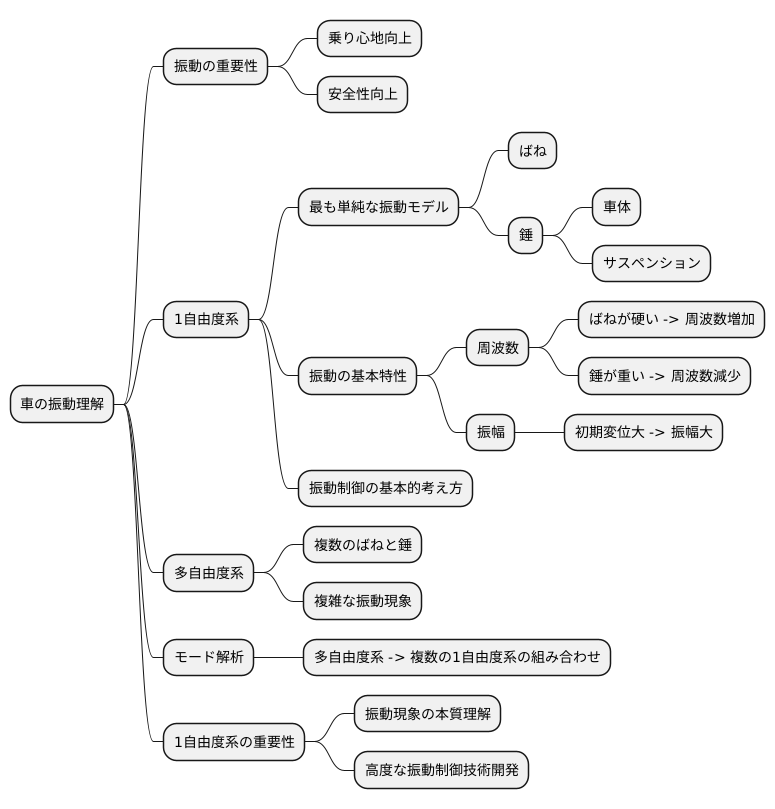
車は、様々な部品が組み合わさってできており、走行中は常に振動しています。この振動を理解することは、乗り心地や安全性を向上させる上で非常に重要です。複雑な車の振動を理解する第一歩として、1自由度系の概念を学ぶことが不可欠です。
1自由度系とは、最も単純な振動モデルで、1つのばねと1つの錘で表現されます。まるで、おもちゃの車のように単純化することで、振動の本質を捉えやすくなります。錘は車体、ばねはサスペンションを模擬していると考えると、車の振動を具体的にイメージできるでしょう。
この単純なモデルを用いることで、振動の回数(周波数)や揺れの大きさ(振幅)といった基本的な特性を理解することができます。ばねが硬ければ振動の回数は多くなり、錘が重ければ振動の回数は少なくなります。また、最初に錘を大きく引っ張れば、揺れの大きさも大きくなります。これらの関係を理解することで、車の振動を制御するための基本的な考え方を学ぶことができます。
しかし、実際の車は1自由度系のように単純ではありません。複数の部品が複雑に繋がっているため、より現実に近い振動を理解するには、複数のばねと錘で表現される多自由度系を考える必要があります。多自由度系では、それぞれの部品が異なる周波数で振動し、互いに影響し合うことで、複雑な振動現象が生じます。この複雑な振動を解析する手法として、モード解析という方法があります。モード解析を用いることで、多自由度系の振動を、複数の1自由度系の振動の組み合わせとして理解することができます。
1自由度系は、車の振動を理解するための基礎となるだけでなく、多自由度系やモード解析といった、より高度な振動解析の土台となります。まずは1自由度系の概念をしっかりと理解し、振動現象の本質を掴むことが、乗り心地や安全性の向上に繋がる、より高度な振動制御技術の開発に繋がります。